[最も選択された] y=x2乗-3 グラフ 315902

2次関数 (3点→頂点) 2次関数の入試問題1 → ｽg ｽﾑ版は別包ｿｽ ｽ ｽ ｽi ｽ ｽ ｽﾎ費ｿｽj ｽQ ｽ ｽ ｽﾖ撰ｿｽ ｽﾌグ ｽ ｽ ｽt ｽm ｽW ｽ ｽ ｽ` ｽn → ｽ ｽ ｽ ｽpPDF ｽﾅは別包ｿｽ y= (x p) 2q ｽﾌグ ｽ ｽ ｽtこの2つの問題について解説をしていきます。 y の変域を求めるのが基礎 それぞれの変域から式を求めるのが応用Y＝x 2 のグラフをx軸方向に＋1平行移動したグラフで、頂点は（1，0）となることがわかります。 では、次の式ではどうでしょうか。 y＝x 2 －2x

最も選択された Yx2乗 1 グラフ ニスヌーピー 壁紙

Y=x2乗-3 グラフ

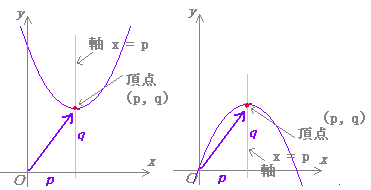
Y=x2乗-3 グラフ-平方根・立方根・3分の2乗の説明 諫早湾の目次 本文に戻る グラフはいずれも，x を横軸，y を縦軸にとってあります．また，負（マイナス）の数は面倒になるので考えないことにします． 2乗と平方根Y = f (x) y = f ( x) のグラフを、 x x 軸方向に p p y y 軸方向に q q 平行移動すると、 y− q = f (x− p) y − q = f ( x − p) になる。 これは、 2 2 次関数以外のあらゆる関数に成り立つことです。 今後も様々なところで出会うことになるでしょう。 なぜこれが

数式のグラフ

放物線のグラフの特徴 放物線グラフの書き方 分数の場合の書き方 y＝ax2乗のグラフ書き方 まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる！ こちらの関連記事はいかがで最後に、一般の2次関数 \y=ax^2bxc\ のグラフについて考えてみよう。たとえば \y=2x^24x1\tag{1}\label{y=ax^2bxcnogurafu}\ のグラフを描くには、次のように式を変形（平方完成 (completing square) という）してから考える。 \begin{align} y=&2x^24x1\\ =&2\left\{x^22x\right\}1\\ &\quad\blacktriangleleft x^2の係数でくくる y=x^22x3の平方完成について(x^22x)3(x1)^24となったのですがなぜ頂点は（1,4）ではなく(1,4)になるのでしょうか？(x1)^2 の項は x=1のとき0、x≠1のとき負は明らかですよね。つまり、(x1)^24 が最も大きなるのは X=1のと

 #グラフ y=x^2 import matplotlibpyplot as plt import numpy as np x = np linspace (5, 5, 100, endpoint = True) #x座標の5〜5まで表示、配列の要素数、endpoint=True（終点を含む） y = x ** 2 y1 = x 3 plt plot (5, 5,下記文献では、「0,∞) で定義された1変数関数 y=f (x)= x 3 」による「非負の実数y」の逆像を立方根と呼ぶ。 ・小平『解析入門I』§23a) (p);n乗根一般。 ・ 松坂『解析入門1』32E例(p113);n乗根一般。 ・赤攝也『実数論講義』§65定義653(p197) 二次関数y=a (xp)^2のグラフ 例として、 y = x2 y = x 2 のグラフを x 軸方向に 1 1 だけ移動したものを考えてみます。 グラフは次のようになります。 グレーが移動前、黒い太線が移動後のグラフです。 各点の移動に注目して、グラフを見ながら点の座標をいく

中3数学。2乗に比例する関数（y ＝ ax²）の「変域」を求めなさい。うわ、変域って何？ 頂点が最小？ 分からん（ガクッ）倒れ込む中学生。立て、立つんだトォォォォ～ッ！ オール5家庭教師、見参ッ！ グイグイ成績が上がる数学のコツ。無料サイトだ。 曲線の式は、X^2＋（Y3√（X^2)）^2＝13√は3乗根の意味です。Xの範囲が、1＜＝X＜＝1 ということ、グラフはY軸を中心として左右対称というところまでは解ったのですが、どうやってグラフを描けばよいかが解 数学 解決済 教えて！goo例題3 y=2x 2 のグラフを x 軸方向に 2，y 軸方向に 1 平行移動してできる曲線の方程式を求めよ。 解答 前の章で行なった平行移動の方法を用いてみます。 y=2x 2 上の任意の点を (x,y) ，平行移動を行なった後の点を (X,Y) とします。すると，

Y X二乗 3のグラフを求めたいのですが どうして頂点が 0 3 になる Yahoo 知恵袋

基本 二次関数 Y Ax 2 のグラフ なかけんの数学ノート

Y=x2乗－2x－2を平方完成したらどうなりますか？ 途中式教えてください 詳説数学Ⅰ第二章 2次関数（前半）～関数とグラフ～ 二次関数y=ax2のグラフの書き方はつぎの3ステップ。 点をたくさんゲット 座標に点をうちまくる 点と点をむすぶ グラフが通る点をたくさんゲットして、 雰囲気で 放物線 をかけばいいのさ。 「グラフ」はたくさんの値＝「点」の集まりの「線」だよね 16年7月11日 年5月14日 基本二次関数 y=ax^2 のグラフ では、二次関数 y = ax2 y = a x 2 のグラフを見ました。 ここでは、この二次関数のグラフを上下に移動したものを考えていくことにします。 目次 平行移動 点の移動 二次関数 ax^2q のグラフ

中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

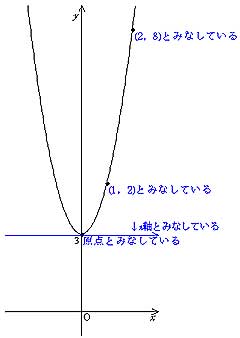
授業実践記録

Y＝x 2 のグラフと同じように、式を満たすxとyの値の組 を座標にとっていくと、点が隙間なくうまって下のよう な滑らかな曲線になるんだ。 ↓曲線になるまで画像をクリック！また、y=x 3 の他にも、y=2x 3 、y=5x 3 ＋1、y=10x 3 ＋x 2 ＋7、y=2x 3 のような、x 3 が含まれている式は3次関数といいます。 3次関数の式がわかったところで、次は、3次関数をグラフに描いて数であるとき，y=g(x) のグラフは y=f(x) のグラフと直線 y=x に関 して対称です（定理77）．81節で述 べたように，関数 √ x ( x≥ 0 ) は関 数x2 ( x≥ 0 ) の逆関数です；従って y= √ x ( x≥ 0 ) のグラフはy=x2 ( x≥ 0 ) のグラフと直線 y=x に関 して対称です． 1次関数

Y X 2 2x 3の平方完成について X 2 2x 3 X 1 2 4 となったので 数学 教えて Goo

関数 グラフ一覧

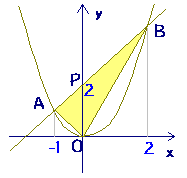
 x2乗＋ (y 3√x2乗)2乗＝1 とありますが，3は係数ではなく 正しい式は x² (y∛x²)²=1 ① で，♡を描きたいのでしょう． ①は陰関数ですが， dy/dx=0 という方程式の実数解を正確に求めることができなければ，増減の様子が分からず，微分法を用いてグラフを直線に見えるもの（定規をあてて点をつないだもの）， y=x 2 のように左側も持ち上がっているもの，右下がりのグラフになっているものは零点です． 3 点 (1, 2) でなく少し上の方の (1, 3) を通っているように見えるグラフは少し減点されます． 45図のように、yがxの2乗に比例する関数のグラフ \(y=x^{2}\)と直線ℓは2点A、Bで交わっている。 2点A、BのX座標はそれぞれ－1、3である。 ABCの面積が OABの面積の2倍となるとき、点Cのx座標を求

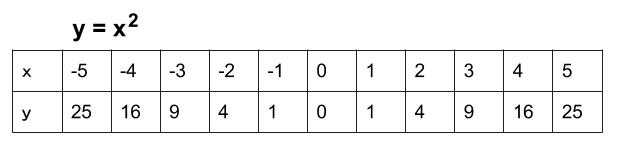
中学数学 Y Ax 2 のグラフ 中学数学の無料オンライン学習サイトchu Su

２次関数 Y A X P のグラフの書き方 グラフの平行移動 数学i By ふぇるまー マナペディア

 y=ax2乗のグラフで覚えておきたい用語 まず、グラフの形は 放物線 となります。 この放物線は左右対称の形となっており、その折れ目となる線のことを 軸 といいます。 また、放物線のてっぺんの部分のことを 頂点 といいます。 かず先生 この3つの用語文献 ・『岩波数学入門辞典』平方根(p543) ・吉田栗田戸田『高等学校数学I』(p53) 上記2文献では、「R＝(－∞,∞） で定義された1変数関数 y=f (x)= x 2 」による実数yの逆像を平方根と呼び、 実数y>0のとき、二つある平方根のうち、正のほうを√yで表すとしている。A,Bの座標が次のそれぞれの場合において、y=ax 2 のグラフが線分AB(両端を含む)と交わるようなaの値の範囲を求めよ。 A(2,1), B(2,8) A(4, 4), B(4, 8) A(3, 1), B(3, 9) 図の放物線lはy= 1 2 x 2 の グラフで、放物線mはy=ax 2 のグラフである。lとmがx軸に平行な直線nと交わる点をそれぞれA, Bとする。Aのx座標が

二次関数のグラフ

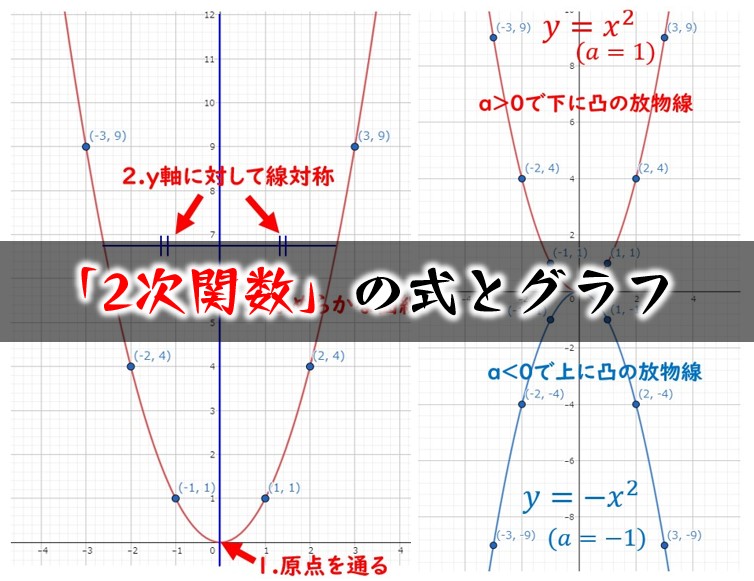
2次関数とは 式とグラフの解説 数学fun

X と y の変域から式を求める; y=2(x3)2乗のグラフはy=①x2乗のグラフをx軸方向に②だけ平行移動したもので、その放物線の軸は直線x=③ 頂点の座標は(④⑤)である。 語群 3,2,3,2,0,1,1,4 上の問題を解いてください！ 全くわかりません>_< 答えは語群の中から選びます。今回は中3で学習する 『 y は x の2乗に比例する y = ax ²』 の単元で、 変域の求め方 について解説していきます。 y の変域を求める;

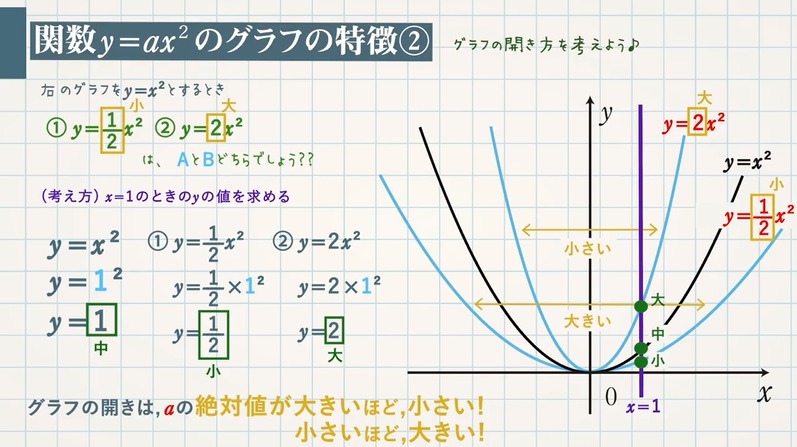
関数y Ax のグラフの性質 教遊者

2乗に比例する関数の変域 無料で使える中学学習プリント

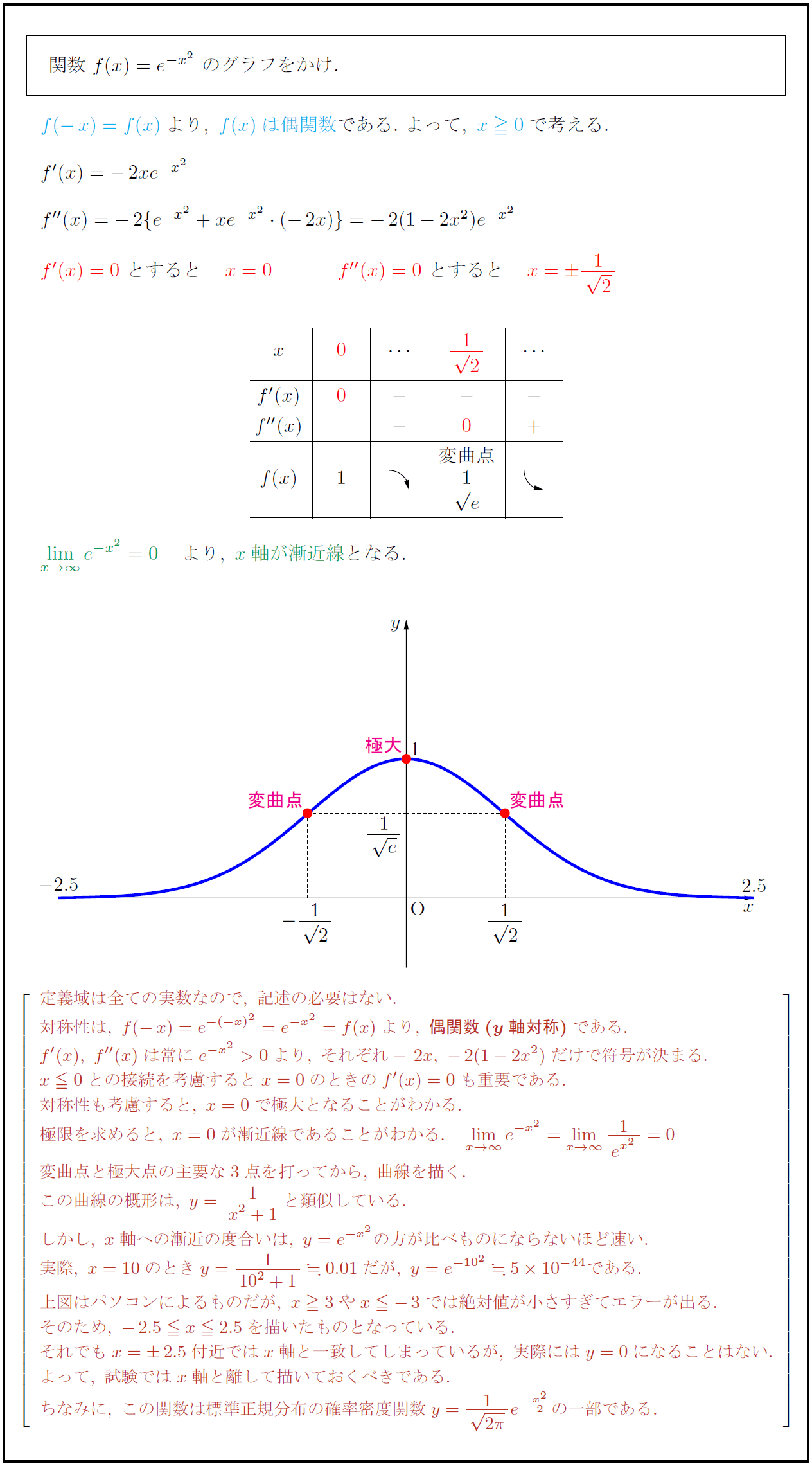
2次関数 y＝x2 のグラフと直線 y＝x＋2 とが交わっているとき，2交点A，Bと原点Oでできる OABの面積の求め方を考えてみます． S1＝2×2÷2＝2です． S2＝2×1÷2＝1です． S＝S1＋S2＝ 3 です． （ OPAの高さは ＋2 です．） 《 問題1 》 次の空欄を埋めなさい2 2次関数の最も簡単な関数は y =x2 y = x 2 である．この関数についてグラフを考える． x x の値3，2，1，0，1，2，3に対する y y の値をを下の表に示す． 各 x x ， y y の組に対応する点を座標平面に描くと左下の図のようになる．表のような y = x2 y = x 2 のY の解として y = arcsin ⁡ x という記法を導入するのです。このような記法を導入することによって, (1) ∫ 0 x 1 − ξ 2 d ξ = 1 2 ( x 1 − x 2 arcsin ⁡ x), のように数式が書けます。もし, a r c s i n を定義していなければ, 上の積分は, \displaystyle\int_0^x\sqrt {1\xi^2

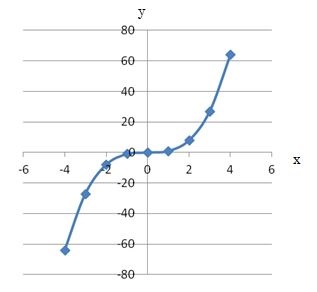
3次関数 方程式 のグラフ もう一度やり直しの算数 数学

２次不等式の解き方 X 4x 5 0 X 4x 5 0の形をした問題 数学i By ふぇるまー マナペディア

Y = a x y 2 = a x y=\sqrt{ax}\iff y^2=ax y = a x y 2 = a x かつ y ≥ 0 y\geq 0 y ≥ 0 なので，グラフは放物線の一部になります（よく見る y = x 2 y=x^2 y = x 2 という放物線を 9 0 ∘ 90^{\circ} 9 0 ∘ 回転させたものの半分）。 b ≠ 0 b\neq 0 b = 0 の場合は平行移動すればよいだけです。例：y=x, y=x, y={2^x} グラフの縮小率を大きくすると、広い範囲が見られます。逆に、縮小率を小さくすると、原点付近を拡大できます。 指数関数について y=x 2 ではなくて、y=2 x としてみます。 指数関数と対数関数は対の関係です。Ex12py def func1 (x, y) return x ** 2 y ** 2 描写データの作成 3次元で描写するには2次元メッシュが必要

Y 1 X ２乗 のグラフってどんなんですか Clearnote

関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ

1

中３ 数学 解き方教えてください 答えは16です お願い致します Clearnote

数学 中3 35 二次関数のグラフ Youtube

2

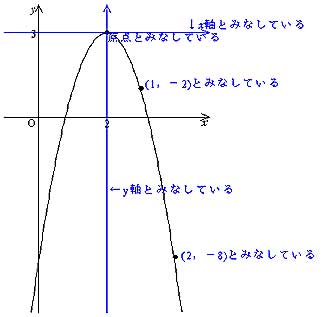
授業実践記録

基礎数学 4回目

数式のグラフ

二次関数のグラフをかけｙ X 2 ２乗頂点 軸おしえてくださ Yahoo 知恵袋

1

3年 関数 Y X のグラフ 数学イメージ動画集 大日本図書

Mathematics 関数と証明 大阪府公立 ２２年前期理数科 働きアリ

Y X2乗 2x 3ってどうしてこの様なグラフになるのでしょうか Yahoo 知恵袋

二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局

F X X２乗 3x 2の解とグラフの答えをお願いいたします 解 って Yahoo 知恵袋

高校数学です 二次関数y X 6xのグラフを書け また その軸と頂点 高校 教えて Goo

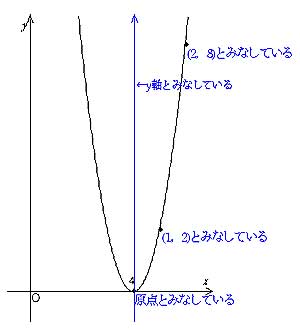
授業実践記録

中3数学 Y X2乗のグラフ 5分で学習 Youtube

例題で学ぶ高校数学 Y Ax2 Q

ｙ ｘ２乗 2ｘ 2を平方完成したらどうなりますか 途中式教えてください Clearnote

Y 1 X2乗のグラフ Youtube

Y ｘ２乗 4x 4のグラフってどうなりますか 頂点と軸と凸 Yahoo 知恵袋

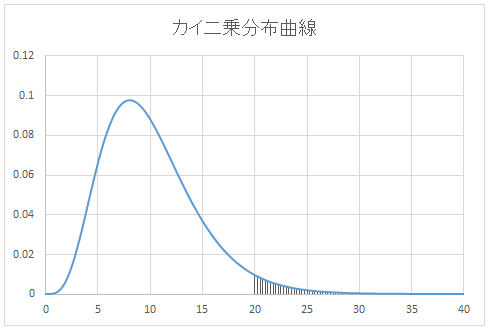
Excelによるカイ二乗分布曲線のグラフの作り方 ブログ 統計web

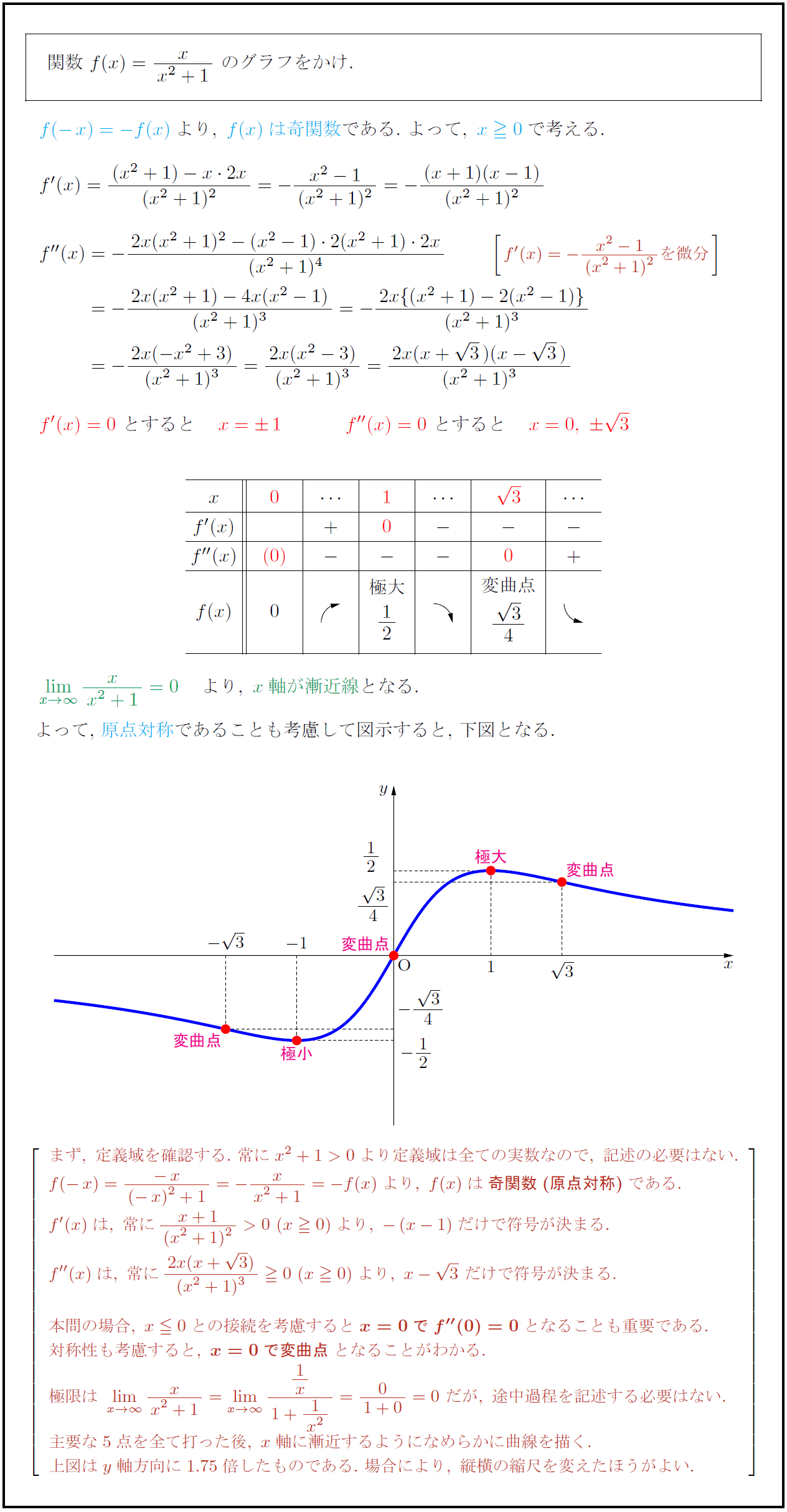
高校数学 分数関数 Y X X 1 のグラフ 受験の月

とまて週報 二次関数で語れ１

Y 3分の1ｘ2乗 2ｘのグラフの ｘ切片の求め方を教えて下さい Y 0のと Clearnote

基本 二次関数y A X P 2のグラフ なかけんの数学ノート

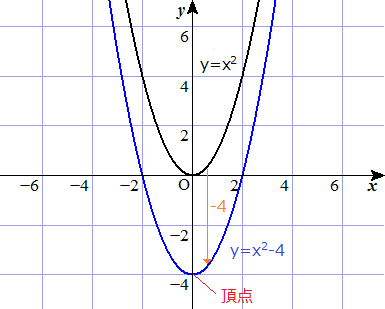
例題で学ぶ高校数学 Y Ax2 Q

1

中学校数学 3年生 数量 2乗に比例する関数 Wikibooks

Aは正の定数とする 関数y X 2 4x 3 0 X A の最大値を求めよ 解き 高校 教えて Goo

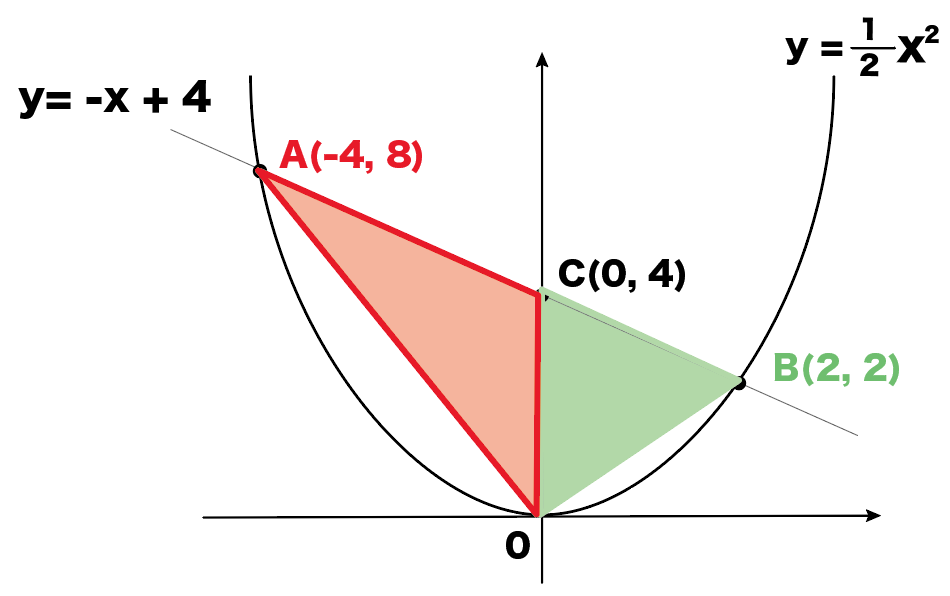
二次関数のグラフで三角形の面積を求める問題の解き方4ステップ Qikeru 学びを楽しくわかりやすく

グラフを教えてください ｙ ｘ二乗 ２ｘ ３ のグラフ Yahoo 知恵袋

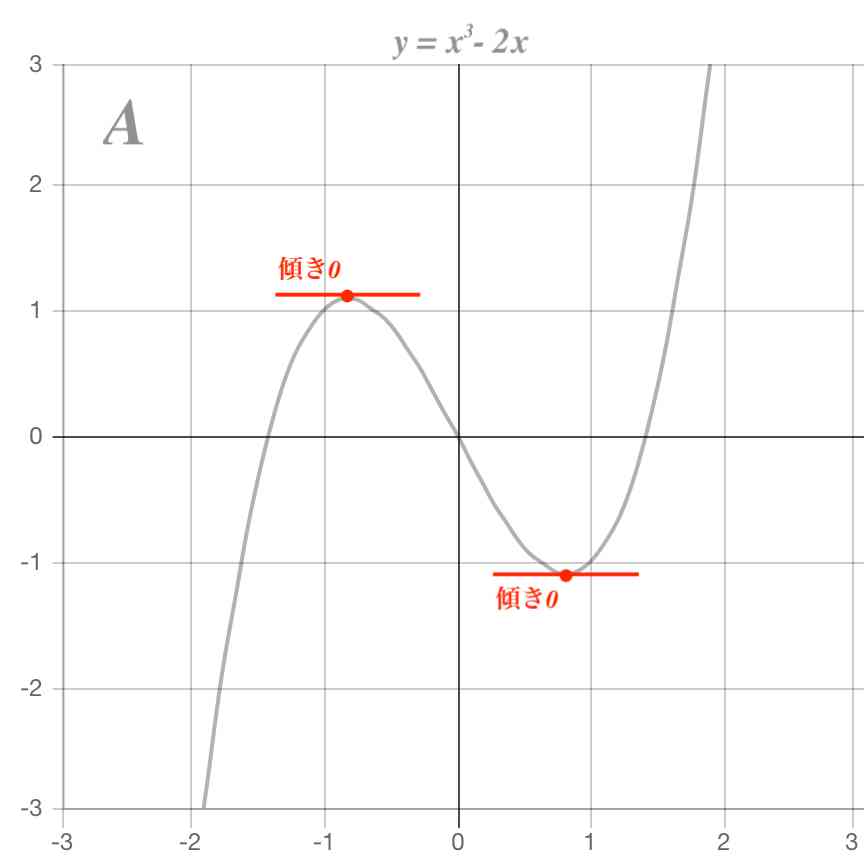
三次関数のグラフの書き方

関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ

中学校数学 3年生 数量 2乗に比例する関数 Wikibooks

基礎数学 4回目

高校数学です 二次関数y X 6xのグラフを書け また その軸と頂点 高校 教えて Goo

基本 無理関数のグラフ 放物線の一部 なかけんの数学ノート

基本 二次関数y A X P 2のグラフ なかけんの数学ノート

二次関数のグラフ 二次不等式 戻る 頂点が原点 0 0 の二次関数グラフは中学3年で学習しました 思い出してください下のグラフは２次関数 つまり は の２乗に比例するグラフ Y Ax2で表します 仮に比例定数 ２として Y 2x2のグラフを書いてみま

Y X2乗 4の式で頂点と軸を求めてグラフを書けと言われました答えはわかるの Yahoo 知恵袋

二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ

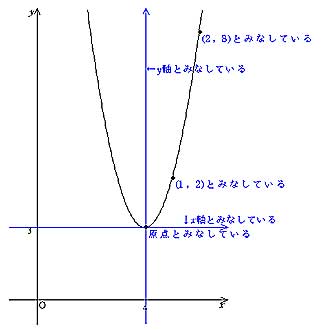
授業実践記録

高校数学 Y Ax 2 Bx Cのグラフ 例題編 映像授業のtry It トライイット

例題で学ぶ高校数学 Y A X P 2

2次関数の問題で Y X２乗 X 1のグラフがこうなるのは何故ですか Yahoo 知恵袋

中3数学 Y X2乗とy X2乗のグラフ 5分で学習 Youtube

最も選択された Yx2乗 1 グラフ ニスヌーピー 壁紙

二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ

この関数のグラフを描きたいのですが 曲線の式は X 2 Y 3 Okwave

最も選択された Yx2乗 1 グラフ ニスヌーピー 壁紙

Y X 2 2x 1のグラフあってるでしょうか 解説のグラフと Yahoo 知恵袋

中３ ２次関数

高校数学 指数関数 Y E X のグラフ 正規分布曲線もどき 受験の月

解説がわかりません なぜｙ ｘ２乗 3ｘを平行移動した放物線の二次関数はｙ Clearnote

関数y X2乗です 図のように Y Ax2乗 Y Bx 7のグラフが Clearnote

中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく

例題で学ぶ高校数学 Y Ax2 Q

上yx2乗 最高のカラーリングのアイデア

２次関数のグラフと直線

Aは正の定数とする Clearnote

中3数学 Y X2乗のグラフの変域 5分で学習 Youtube

２乗に比例するグラフ 中学から数学だいすき

2次関数 変域 変域からの式の決定 基 標 数学の解説と練習問題

2次関数のグラフ 2次関数のグラフの式の 頂点の求め方を教えて下さい Okwave

上yx2乗 最高のカラーリングのアイデア

中3数学 Yはxの2乗に比例 とは 映像授業のtry It トライイット

関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ

2次関数のグラフ Y X 2

中学数学 Y Ax 2 のグラフ 中学数学の無料オンライン学習サイトchu Su

２乗に比例するグラフ 中学から数学だいすき

3分の２乗の説明

二次関数の移動

因数分解とグラフ 中学から数学だいすき

2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ

二乗に比例とは 1分でわかる意味 式 グラフ 例 比例との違い

2次関数のグラフと直線

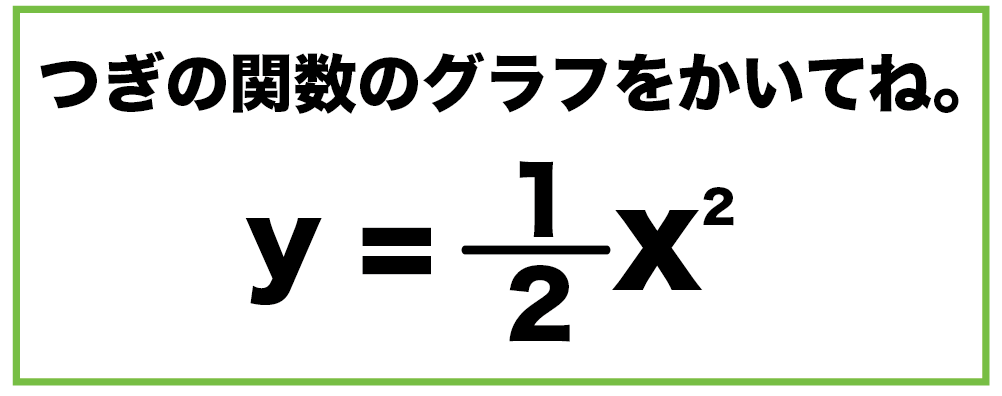
中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ

2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ

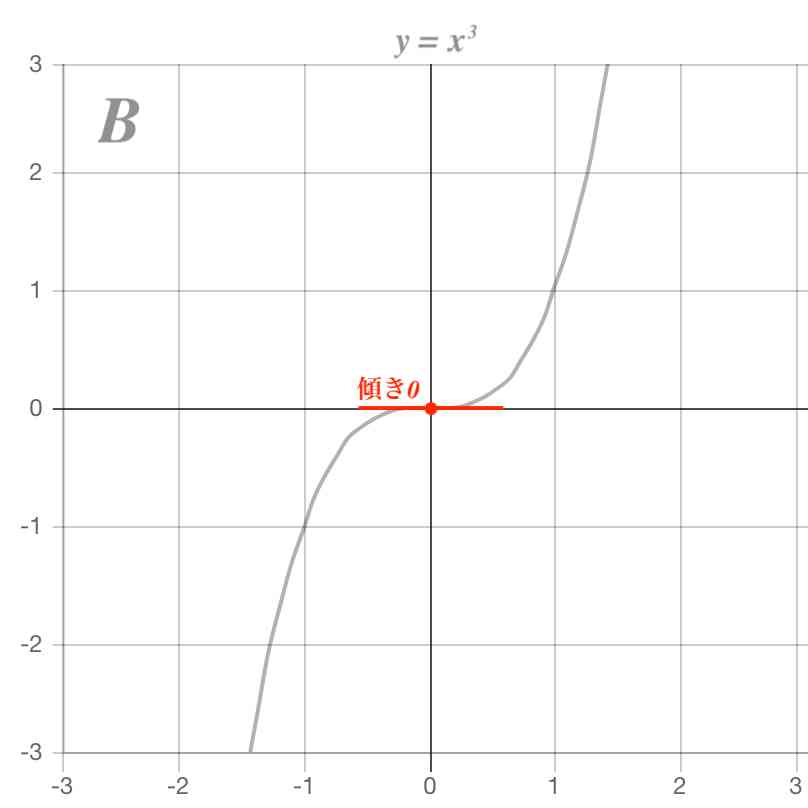
三次関数のグラフの書き方

対数グラフ

Y 3分の1xの2乗の関数のグラフはどのようにしてかけばいいの Yahoo 知恵袋

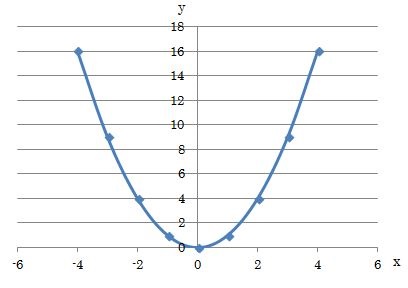
2次関数 方程式 のグラフ もう一度やり直しの算数 数学

２次関数の最大値 最小値

二次関数のグラフ

中3数学 Y Ax2乗の変域の求め方を解説 数スタ

２次関数のグラフ